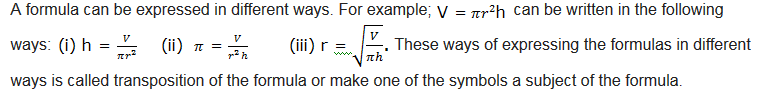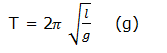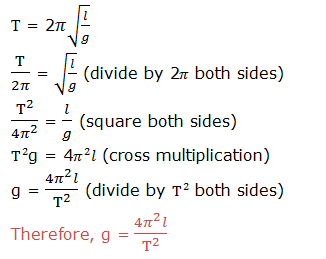TOPIC 1: EXPONENTS AND RADICALS ~ MATHEMATICS FORM TWO
Exponents
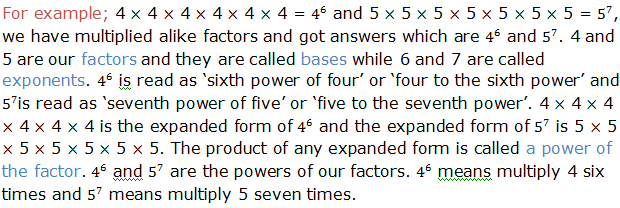


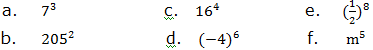
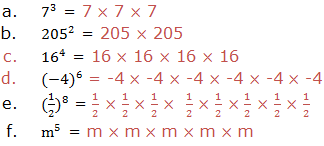
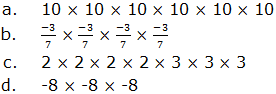
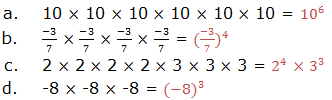
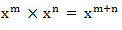
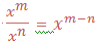
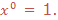
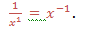
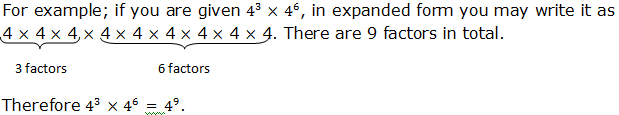
when we multiply powers having the same base, we add their exponents.
If x is any base and m and n are the exponents, therefore:
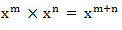
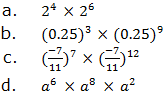
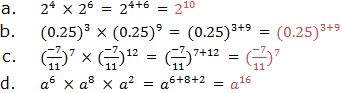
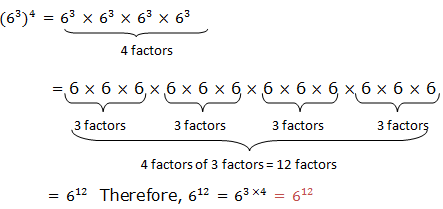
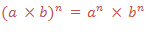
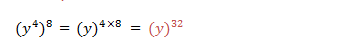
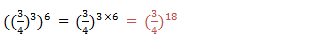
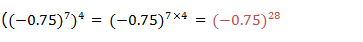
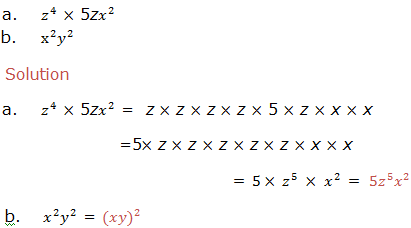
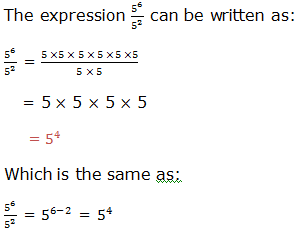
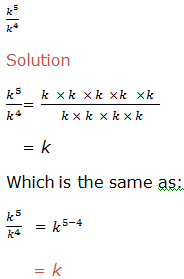
to divide powers of the same base we subtract their exponents (subtract
the exponent of the divisor from the exponent of the dividend). That
is,
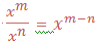
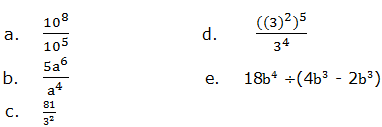
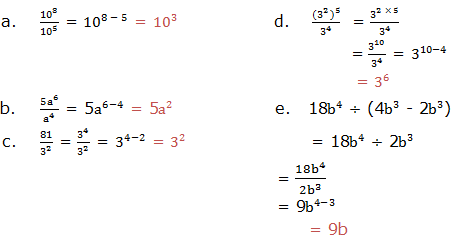
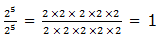
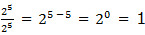
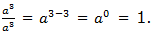
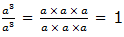


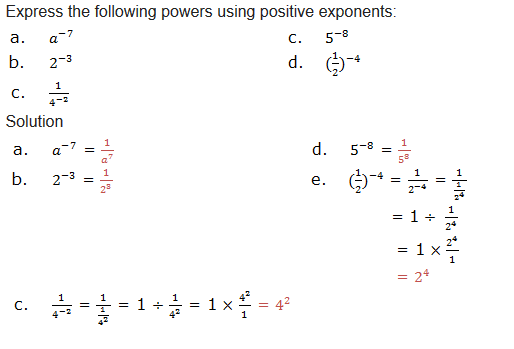


- 169
- 81
- 10,000
- 625

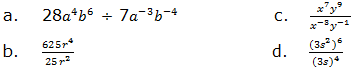
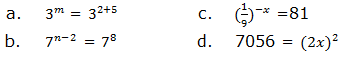
- Base 4
- Base 8
- Base 2
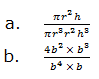


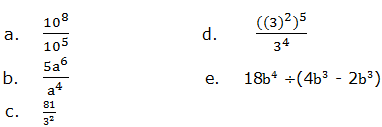
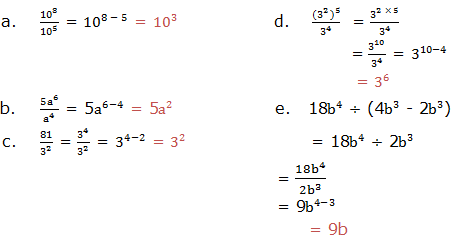
Radicals
are opposite of exponents. For example when we raise 2 by 2 we get 4
but taking square root of 4 we get 2. The same way we can raise the
number using any number is the same way we can have the root of that
number.
For example, square root, Cube root, fourth root, fifth roots
and so on. We can simplify radicals if the number has factor with root,
but if the number has factors with no root then it is in its simplest
form. In this chapter we are going to learn how to find the roots of the
numbers and how to simplify radicals.
a number is expressed as a product of equal factors, each of the
factors is called the root of that number. For example,25 = 5× 5;so, 5
is a square root of 25: 64 = 8× 8; 8 is a square root of 64: 216 = 6 ×6
×6, 6 is a cube root of 216: 81 = 3 × 3 ×3 ×3,3 is a fourth root of 81:
1024 = 4 ×4 ×4 ×4 ×4, 4 is a fifth root of 1024.
Therefore, the nth root of a number is one of the n equal factors of that number. The symbol for nth root isn√
where√is called a radical and n is the index (indicates the root you
have to find). If the index is 2, the symbol represents square root of a
number and it is simply written as√without the index 2.n√pis expressed in power form as,
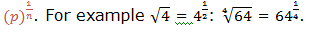


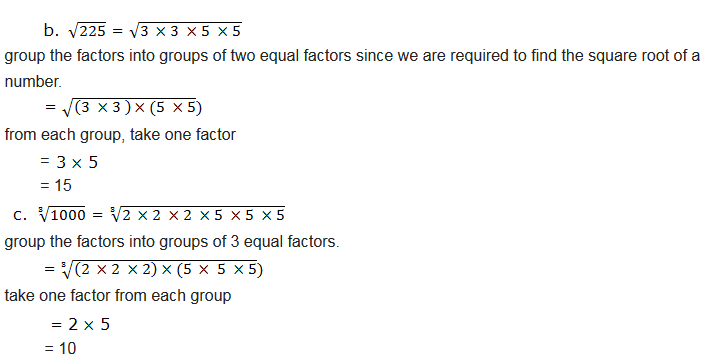
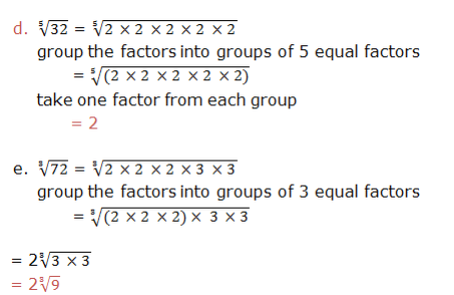
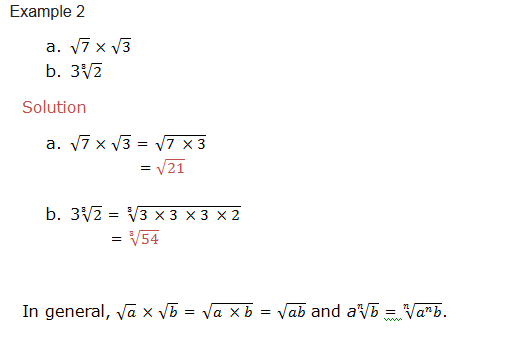
Basic Operations on Radicals
Perform basic operations on radicals
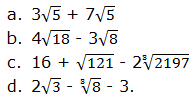
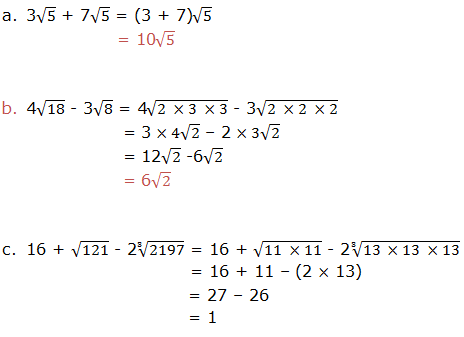
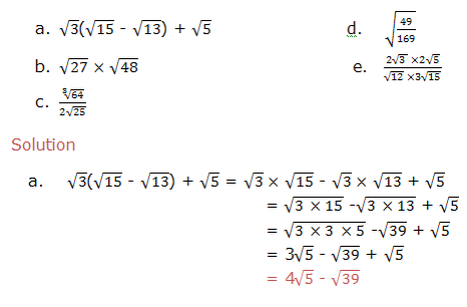
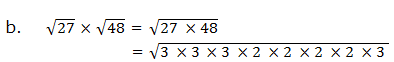
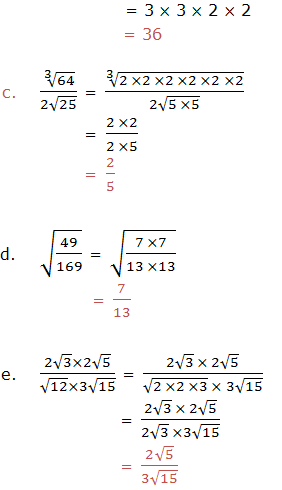
The Denominator
you are given a fraction expression with radical value in the
denominator and then you express the expression given in such a way that
there are no radical values in the denominator, the process is called
rationalization of the denominator.


rationalize these fractions, we have to multiply by the fraction that
is equals to 1. The factor should be considered by referring the
difference of two squares.

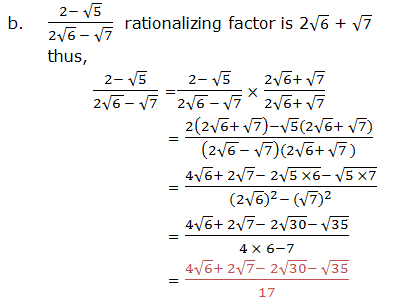




Square Roots and Cube Roots of Numbers from Mathematical Tables
Read square roots and cube roots of numbers from mathematical tables
If
you are to find a square root of a number by using Mathematical table,
first estimate the square root by grouping method. We group a given
number into groups of two numbers from right. For example; to find a
square root of 196 from the table, first we have to group the digits in
twos from right i.e. 1 96. Then estimate the square root of the number
in a group on the extreme left. In our example it is 1.
The square root
of 1 is 1. Because we have two groups, this means that the answer has
two digits before the decimal point. Our number is 196, read 1.9 in the
table on the extreme left. From our number, we are remaining with 6, now
look at the column labeled 6. Read the number where the row of 1.9 meet
the column labeled 6. It meets at 1.400.
Therefore the square root of
196 = 14.00 since we said that the answer must have2 digits before
decimal points. Note: If you are given a number with digits more than 4
digits. First, round off the number to four significant figures and then
group the digits in twos from right. For example; the number 75678 has
five digits. When we round it off into 4 digits we get 75680 and then
grouping into two digits we get 7 56 80.
This shows that our answer has 3
digits. We start by estimating the square root of the number to the
extreme left, which is 7, the square root of 7 is between 2 and 3. Using
the table, along the row 7.5, look at the column labeled 6. Read the
answer where the row 7.5 meets the column 6. Then go to where it is
written mean difference and look at the column labeled 8, read the
answer where it meets the row 7.5.
Take the first answer you got where
the row 7.5 met the column 6 and add with the second answer you got
where the row 7.5 met the column 8 (mean difference column). The answer
you get is the square root of 75680. Which is 275.1
Transposition of Formula