TOPIC 4: LOGARITHMS ~ MATHEMATICS FORM 2
We always ask ourselves, how many of one number do we multiply to get another number?
Standard Form
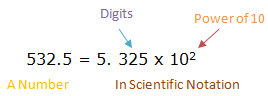
- Thedigits(with the decimal point placed after the first digit) followed by
- X 10 to a powerthat puts a decimal point where it should be (i.e. it shows how many places to move the decimal point).
Numbers in Standard Form
Write numbers in standard form
- When the number is 10 or greater, the decimal place has to move to the left
and the power of 10 will be positive. For example; 47 055 = 4. 7055 x 104 - When the number is smaller than 1, the decimal point has to move to the right and the power of 10 will be negative. For example;
that: After putting the number in scientific notation make sure that
the digits part is between 1 and 10 (it can be 1 but never 10). And the
power part shows exactly how many places to move the decimal point.
Computations which Involved Multiplication and Division of Numbers Expressed in Standard Form
Perform computations which involved multiplication and division of numbers expressed in standard form
Definition of a logarithm
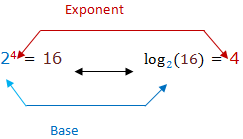
A logarithm answers the question: How many of one number do we multiply to get another number. For example; how many of 2s do we multiply to get 16? Answer: 2 x 2 x 2 x 2= 16 so we needed to multiply 4 of the 2s to
get 16. So the logarithm is 4.
The two things are the same:

The
number we are multiplying is called the base. So we can say ‘the
logarithm of 16 with base 2 is 4’ or ‘log base 2 of 16 is 4’ or ‘the
base-2 log of 16 is 4’.
- The base (the number we are multiplying in our example it is 2)
- How many times to use it in multiplication (in our example it is 4 times, which is the logarithm)
- The number we want to get (in our example it is 16)
There
is a relationship between the exponents and logarithms. The exponent
says how many times to use the number in a multiplication and logarithm
tells you what the exponent is. See the illustration below:

Laws Of Logarithms
The Laws of Logarithms
State the laws of logarithms
There
are several laws of logarithms which help in evaluating them. These
laws are valid for only positive real numbers. The laws are as follows:
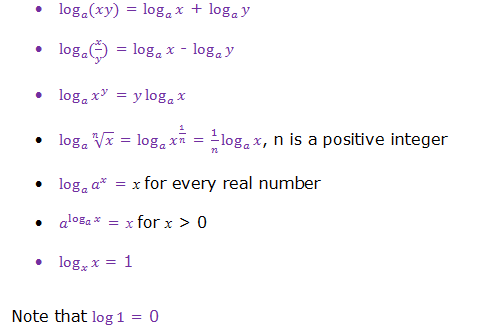
Verification of the Laws of Logarithms Using the Knowledge of Exponents
Verify the laws of logarithms using the knowledge of exponents
Example 2
Use the laws of logarithms to evaluate the following:
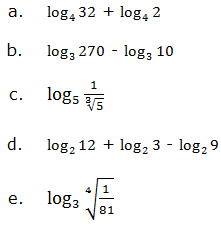
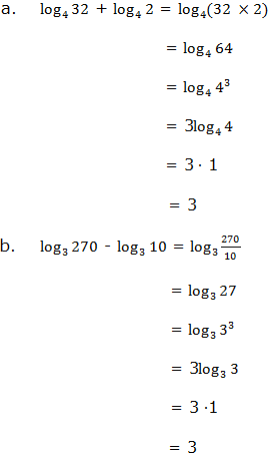
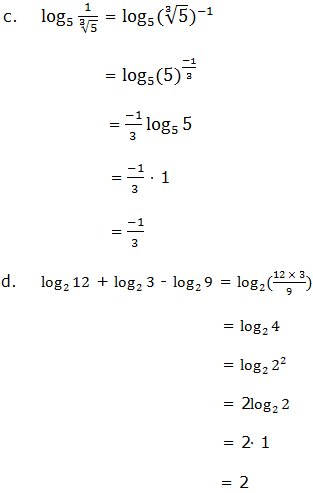
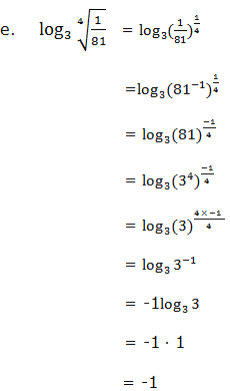
Change of base
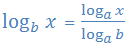
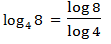
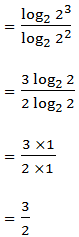
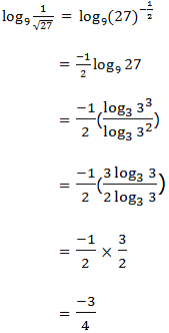
Logarithms to Base 10


Logarithmic Equation
Solve logarithmic equation
Use the laws of logarithms to evaluate the following:
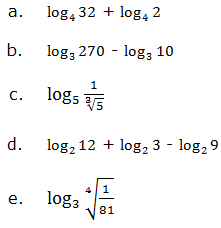
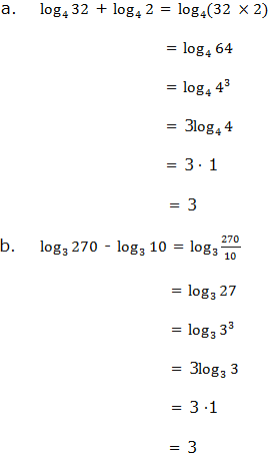
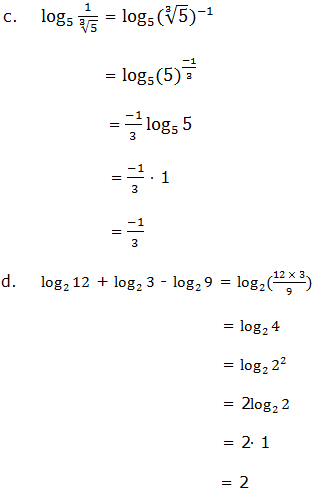
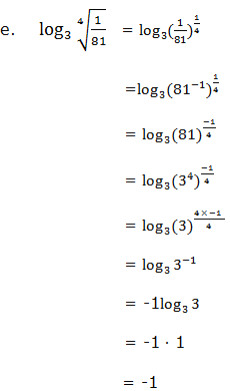
Laws of Logarithms to Find Products, Quotients, Roots and Powers of Numbers
Apply laws of logarithms to find products, quotients, roots and powers of numbers
Here
we deal with all 4 operations which are addition, subtraction,
multiplication and division. All operations are just as usual operations
except division when we are given a negative characteristic. For
example;


of the logarithmic tables are of base 10 (common logarithms). When we
want to read a logarithm of a number from logarithmic table, we first
check if the number is between 0 and 10 (but not 0 or 10) because the
table consists only of logarithms of numbers between 0 and 1.
For
example; what is the logarithm of 5.25 from the table. Our number is
between 0 and 1. We look at the most left column and find where 52 is
(we ignore the decimal point). Then slide your finger along this row to
the right to find column of the next digit in our example is 5. Read the
number where the row of 52 meets the column of 5. The logarithm of 5.25
is 0.7202.
If
the number has 4 digits like 15.27, we do the following. First of all,
checking our number we see that it is greater than 10. The number is
between 10 and 100. And we know that the logarithm of 10 is 1 and
logarithm of 100 is 2. So logarithm of 15.27 is between 1 and 2,
normally less than 2 but greater than 1, hence 1.something.
That
something we need to find it in a logarithm table. Look at the most left
column the row labeled 15, then, slide your finger to the right to find
the column labeled 2. Read the number where the row of 15 meets the
column of 2, the number is 0.1818. We are remaining with one digit which
is 7. If your log table has a part with mean difference table, slide
your finger over to the column in that table marked with the next digit
of the number you are looking up, in our example it is 7.
Slide over to
row 15 and mean difference 7. The row of 15 meets mean difference column
7 at number 20. Add the two numbers obtained (the mean difference
number is added to the last digits of our first number we obtained) i.e.
0.1818 + 20 = 1838. Now add characteristic which is 1 since 15.27 is
between 10 and 100. We get 1 +0.1838 = 1.1838. Therefore Log 15.27= 1.1838.
that if you are given a number with more than 4 digits, first round off
the number to 4 digits and then go on with similar procedures as
explained in examples above.
To
find the number whose logarithm is known, we can call it ant-logarithm
the same logarithmic table can be used. For example to find the number
whose logarithm is 0.7597, look at the central part of the log table
find the number (mantissa) 7597. This is in the intersection of the row
labeled 57 and column 5. So the number is 575. But in order to get
correct answer we have to consider characteristic of our logarithm which
is 0. This means our number is between 0 and 10 because the numbers
whose logarithms are 0.something are between 0 and 10. Hence, we need to
place one decimal point from left to our number to make it be between 0
and 10. Therefore the number will be 5.75 i.e. log 5.75 = 0.7597, thus
antilog 0.7597= 5.75.
How to find the ant-log
Understand the ant-log table. Use it when you have log of a number but
not the number itself. the ant-log is also known as the inverse log.
Step 2:
Write down the characteristic. This is the number before decimal point.
If you are looking up the ant-log of 2.8699, the characteristic is 2.
Remove it from the number you are looking up. But never forget it
because it will be used later. So it is better if you write it
somewhere.
Find the row in the most left column that matches the first two numbers
of the mantissa. Our mantissa is 8699. So run your finger down that
column until you find .86.
Slide your finger over to the column marked with the next digit of the
mantissa. For 2.8699, slide your finger along the row marked .86 to find
the intersection with column 9. This reads 7396. Write this down.
If your ant-log table has a table of mean difference, slide your finger
over to the column in that table marked with the next digit of the
mantissa. Make sure to keep your finger in the same row. Considering our
example, slide your finger over the to the last column in the table,
column 9. The intersection of row .86 and mean difference column 9 is
15. Write it down.
Add the two numbers obtained from the two previous steps. In our
example, these are 7396 and 15. Adding them i.e. 7396 + 15 = 7411.
Step 7:
Use characteristic to place decimal point. Our characteristic is 2,
which means our answer is between 100 and 1000 because log 100 = 2 and
log 1000 = 3. For the number 7411 to fall between 100 and 1000, the
decimal point should be placed after 3 digits. So, the final answer is
741.1 therefore the ant-log of 2.8699 is 741.1.
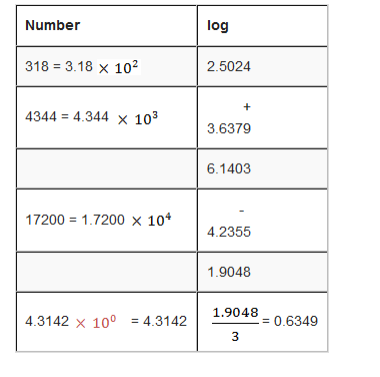
Find the product of 25.75 ×450.
Logarithmic laws we saw that multiplication of two numbers is the same
as addition of two the same two numbers. How to do it?
If we set our example in tabular form it will look like this:

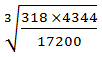
















































Thank you for content. Area rugs and online home decor store. Hello Administ .
Merhaba admin gerçekten çok güzel bir site olmuş. Beğendim. Thank you very much 🙂
Selamlar harika bir blog. Çok beğendim. Google’yi de çok seviyorum 🙂
Hello my frends. İts web site too like. Thank you very nice admin:)