Home MATHEMATICS TOPIC 9: TRIGONOMETRY ~ MATHEMATICS FORM 2

TOPIC 9: TRIGONOMETRY ~ MATHEMATICS FORM 2

1717

TOPIC 9: TRIGONOMETRY ~ MATHEMATICS FORM 2

Do you want to learn the relationships involving lengths and Angles of right-angled triangle? Here, is where you can learn.

Trigonometric Rations

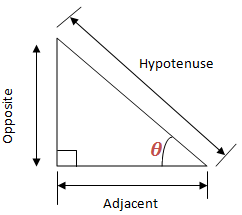
Trigonometry is all about Triangles. In this chapter we are going to deal with Right Angled Triangle. Consider the Right Angled triangle below:

The sides are given names according to their properties relating to the Angle .

Adjacent side is adjacent (next to) to the Angle

Opposite side is opposite the Angle

Hypotenuse side is the longest side

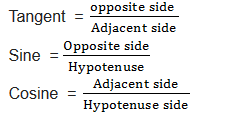
Sine, Cosine and Tangent of an Angle using a Right Angled Triangle

Define sine, cosine and tangent of an angle using a right angled triangle

Trigonometry is good at finding the missing side or Angle of a right angled triangle.

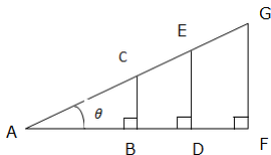
The special functions, sine, cosine and tangent help us. They are simply one of a triangle divide by another. See similar triangles
below:

The ratios of the corresponding sides are:

Where by t, c and s are constant ratios called tangent (t), cosine (c) and sine (s) of Angle respectively.

The right-angled triangle can be used to define trigonometrical ratios as follows:

The short form of Tangent is tan, that of sine is sin and that of Cosine is cos.

The simple way to remember the definition of sine, cosine and tangent is the word SOHCAHTOA.

This means sine is Opposite (O) over Hypotenuse (H); cosine is Adjacent (A) over Hypotenuse (H); and tangent is Opposite (O) over Adjacent (A). Or

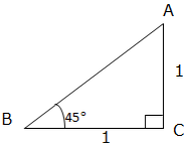
Example 1

Given a triangle below, find sine, cosine and Tangent of an angle indicated.

Solution

Example 2

Given that

Trigonometric Ratios of Special Angles

Determination of the Sine, Cosine and Tangent of 30°, 45° and 60° without using Mathematical Tables

Determine the sine, cosine and tangent of 30°, 45° and 60° without using mathematical tables

The special Angles we are going to deal with are 30⁰, 45⁰, 60⁰, 90⁰. Let us see how to get the Tangent, Sine and Cosine of each angle as follows:

First, consider an equilateral triangle ABC below, the altitude from C bisects at D.

AD = BD = 1 (bisection)

The results above can be summarized in table as here below:

Simple Trigonometric Problems Related to Special Angles

Solve simple trigonometric problems related to special angles

Example 3

Find the value of x if

Trigonometric Tables

The Trigonometric Ratios from Tables

Read the trigonometric ratios from tables

We
can find the trigonometrical ratio of any angle by reading it on a
trigonometrial table in the same way as we did in reading logarithm of a
number on a logarithimic table.

The
angle is read from the extreme left hand column and then the
corresponding value under the corresponding column of minutes and
seconds whenever there is seconds. If we are given angle with zero
minute (0’), we read the corresponding value of an angle under the
column labeled 0’.

For example; if we are to find the sin56⁰, we have to go to the column extreme to the left. Run your finger down until you meet56⁰, then slide your finger to the exactly same raw to the column labeled 0’. The answer will is 0.8290.

Another example: find cos 78⁰45′. Read the angle78⁰
to the column extreme to the left and then slide your figure to the
exactly same angle until you meet the column labeled 45’. The table I’m
using has no 45’, so, I have to read the number near to 45’. This number
is 42’. The answer of cos78⁰42’is 0.1959. the minutes
remained, we are going to read them to the difference columns. Slide
your figure to the same column of degree78⁰to the difference
column labeled 3’ (minutes remained). The answer is 9. But the
instructions says, ‘numbers to the difference columns to be subtracted,
not added’. This means we have to subtract 9 (0.0009) from 0.1959. When
we subtract we remain with 0.1950. Therefore, cos78⁰45’= 0.1950.

Note that, you can read in the same way the tangent of an angle as we read cosine and sine of an angle. Make sure you read the tables of Natural sine or cosine and or tangent and not otherwise.

Problems involving Trigonometric Ratios from Tables

Solve problems involving trigonometric ratios from tables

Example 4

Use table to find the value of:

sin 55⁰
cos 34.4⁰
tan 60.2⁰

Solution

sin 55⁰ = 0.8192

To find the value of cos 34.4⁰ , first change34.4⁰ into degrees and minutes. Let us change the decimal part i.e. 0.4⁰ into minutes. 0.4 ×60 minutes = 24 minutes thus, cos 34⁰24′ = 0.8251

To find the value of tan 60.2⁰, first change60.2⁰ into degrees and minutes. Let us change the decimal part i.e. 0.2⁰ into minutes. 0.2 ×60 minutes = 12 minutes thus tan 60⁰12′ = 1.7461

Important note: when finding the inverse of any of the three trigonometric ratios by using table, we search the given ratio on a required table until we find it and then we read the corresponding degree angle.

It is the same as finding Ant-logarithm of a number on a table by searching.

Angles of Elevation and Depression

Angles of Elevation and Angles of Depression

Demonstrate angles of elevation and angles of depression

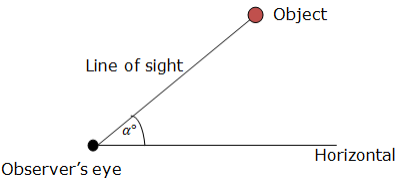
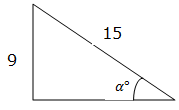
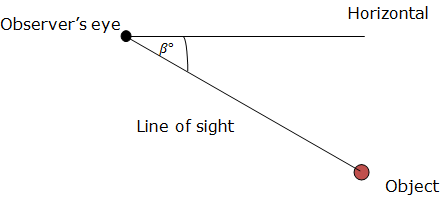
Angle of Elevation of an Object as seen by an Observer is the angle between the horizontal and the line from the Object to the Observer’s aye (the line of sight).

See the figure below for better understanding

The angle of Elevation of the Object from the Observer is α⁰.

Angle of depression of an Object which is below the level of Observer is the angle between the horizontal and the Observer’s line of sight.

To have the angle of depression, an Object must be below the Observer’s level. Consider an
illustration below:

The angle of depression of the Object from the Object is β⁰

Problems involving Angles of Elevation and Angles of Depression

Solve Problems involving angles of elevation and angles of depression

Example 5

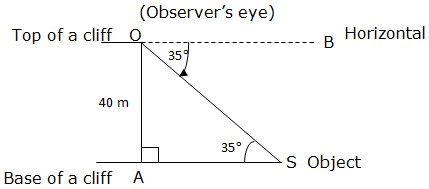
From the top of a vertical cliff 40 m high, the angle of a depression of an object that is level with the base of the cliff is35⁰. How far is the Object from the base of the cliff?

Solution

We can represent the given information in diagram as here below:

Angle of depression = 35⁰

Exercise 1

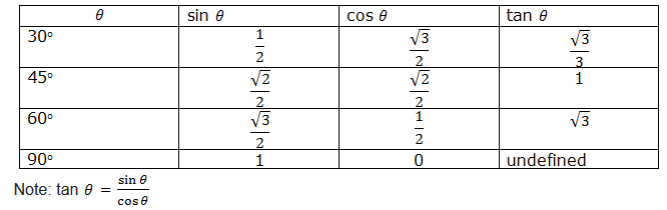
1. Use trigonometric tables to find the following:

cos 38.25⁰
sin 56.5⁰
tan 75⁰

2. Use trigonometrical tables to find the value of x in the following problems.

sin x⁰ = 0.9107
tan x⁰ = 0.4621

3. Find the height of the tower if it casts a shadow of 30 m long when the angle of elevation of the sun is38⁰.

4. The Angle of elevation of the top of a tree of one point from east of it and 56 m away from its base is25⁰. From another point on west of the tree the Angle of elevation of the top is50⁰. Find the distance of the latter point from the base of the tree.

5. A ladder of a length 15m leans against a wall and make an angle of30⁰with a wall. How far up the wall does it reach?

2 COMMENTS

staples scientific calculator 21/08/2022 at 15:05

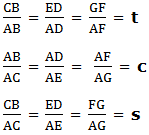
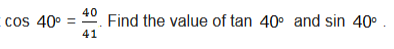
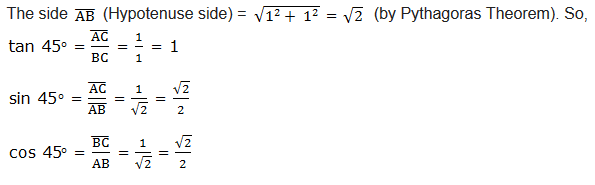
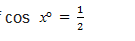
Howdy! I know this is kinda off topic but I was wondering which blog platform are
you using for this site? I’m getting sick and tired of WordPress because I’ve had issues with
hackers and I’m looking at alternatives for another platform.
I would be awesome if you could point me in the direction of a good platform.

Martin 22/05/2021 at 06:02

How to download the notes