TOPIC 10: INTEGRATION | MATHEMATICS FORM 5

INTEGRATION

Integration :Is the reverse process of differentiation, i.e. the process of finding the expression for y in terms of x when given the gradient function.

The symbol for integration is  , denote the integrate of a function with respect to x

If 

This is the general power of integration it works for all values of n except for n = -1

Example

1.      

2.       Integrate the following with respect to x
(i)3x²

Solution

  Integration of constant

The result for differentiating c x is c

Properties

(1)  

(2)  

Integration by change of variables

If x is replaced by a linear function of x, say of the form ax + b, integration by change of variables will be applied
E.g.     

Considering  in similar way gives the general result

 

Example

Find the integral of the following

a) (3x – 8) ⁶              b) 

Solution (a)

Solution (b)

→ If 

 

Example

1.   Find  

Solution

2.   Find 

Solution

Integration of exponential function

Example 01

Solution

Alternative

Example 02

Solution

Alternative

Integrating fraction

If  

Differentiating with respect to x gives

Example

1.    ,given that f(x)=x²+1

 

Solution

2.      Find 

solution

Note: 2x  is the derivative of x² + 1 in this case substitution is useful

i.e. let u = x² + 1

This converts into the form     

 

Standard integrals

·        

·        

·        

·        

·         →∫sec x tan xdx=sec x+c

·        

·        

·        

·        

·        

·        
·       

·        

EXERCISE

Find the integral of the following functions

i)  

ii)   

iii)  

iv)  

 

Integration by partial fraction

Integration by partial fraction is applied only for proper fraction

E.g.  

Note that:

The expression is not in standard integrals

 

Example 01

Example 02

 

Improper fraction

If the degree of numerator is equal or greater than of denominator, adjustment must be made

Example

1.      Find  

Solution

Both numerator and denominator have the degree of 2

2.      

3.      

If the denominator doesn’t factorize, splitting the numerator will work

→ Numerator = A (derivative of denominator) + B

Example

Solution

Important

It can be shown that

EXERCISE

I.            

II.            

III.            

Integrated of the form

Note that:

1. If the denominator has two real roots use partial fraction

2. If the denominator has one repeated root use change of variable or recognition

3. If the denominator has no real roots, use completing the square

E.g.

I.            

II.      

III.     

Integral of the form

Example
→ 

Then hyperbolic function identities is identities is used 

Note that:

If the quadratic has 1 represented root, it is easier

E.g.

EXERCISE

Find the following

i.      

ii.    

iii.   

iv.   

v.    

Integration of Trigonometric Expression
Integration of Even power of  
Note that: for even power of   use the identity
i) 
ii) 

Example 01

Find  

Example 02

  Odd powers of 

For odd powers of   use identity 

Example

Find    




   Any power of tan

The identity   is useful as it is the fact that   It will be understood that;

Example:

1.                  Find  

  Solution:

2.      

solution

Multiple Angles

To integrate such type of integral, one of the factor formulae will be used

1.  

2.  

3. 

4.  

Example

1.      Find 

Solution

2. 

Solution

EXERCISE

Find the integral of the following

1. 

2.   

3.  

4. Integrated by change of variables 

 

1.      

Note that

For integrand containing   and  , or even powers of these, the change of variable    can be used.

Example

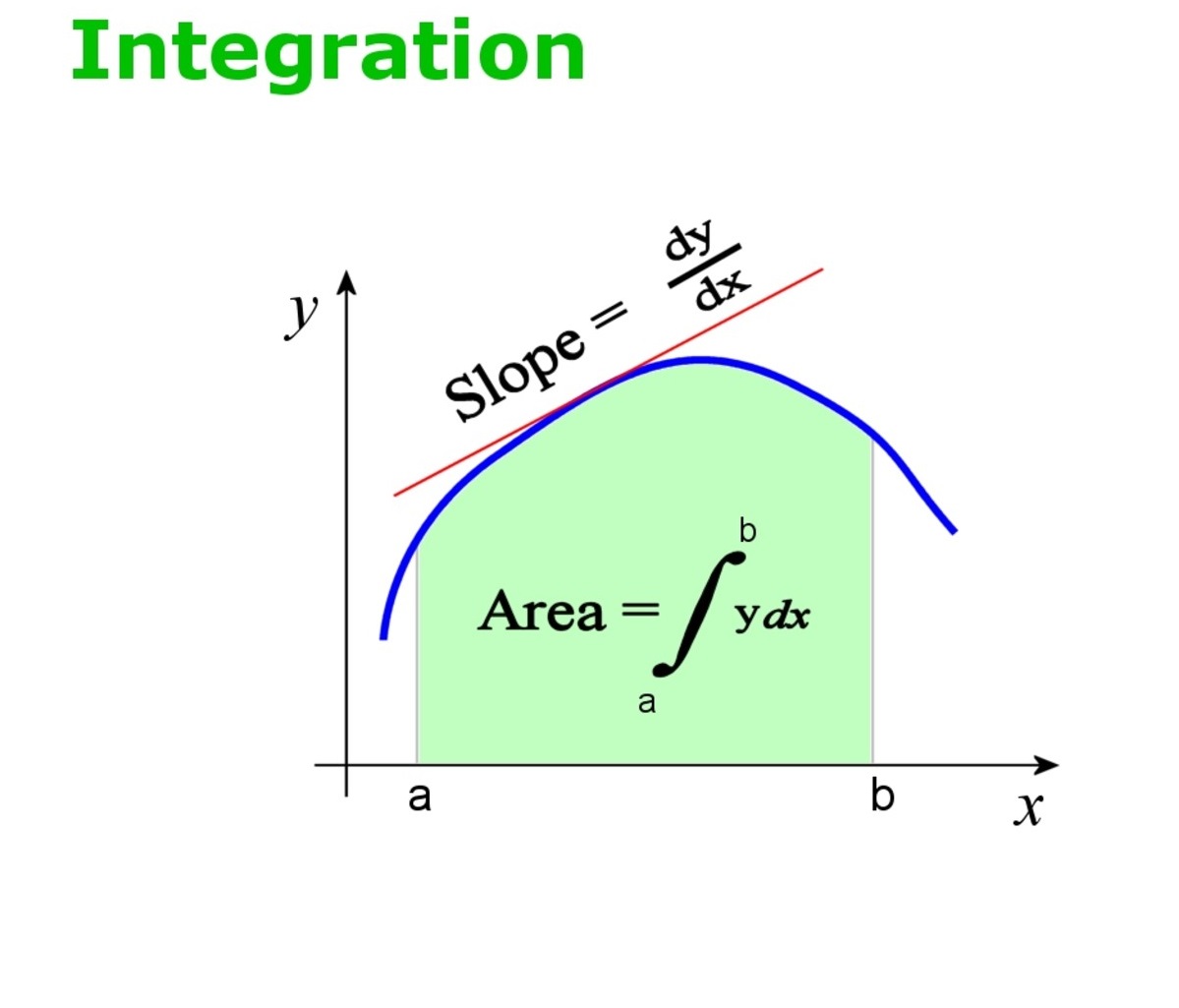
APPLICATION OF INTEGRATION

 

To determine the area under the curve

 

Given A is the area bounded by the curve y=f(x) the x -axis and the line x=0 and x=b where b> a

 

The area under that curve is given by the define definite integral of f(x) from a to b

= f (b) – f (a)

Examples

1. Find the area under the curve f(x) =x²+1 from x=0 to x=2

2. Find the area under the curve f(x) = from x=1 to x=2

3. Find the area bounded by the function f(x) =x ²-3, x=0, x=5 and the x- axis

Solution

1. f(x) =  + 1

y intercept=1

 

 

 

EXERCISE

1.      Find the area between y = 7-x² and the x- axis from x= -1 to x=2

2.      Find the area between the graph of y=x² x – 2 and the x- axis from x= -2 to x=3

Solution

^1.        y =7-x²

Where y- intercept =7

= 6.67 + 11.3

=17.97sq units

Volume of the Solids of Revolution

The volume,V of the solid of revolution is obtained by revolving the shaded portion under the curve, y= f(x) from x= a to x =b about the x -axis is given by

Example 1

Find the volume of revolution by the curve y=x² from x=0 to x=2 given that the rotation is done about the the x- axis

 

Exercise

1. Find the volume obtained when each of the regions is rotated about the x – axis.

a) Under  y= x³, from x =0 to x=1
b) Under y²= 4-x, from x=0 to x=2
c)Under y= x², from x=1 to x=2
d)Under y= √x, from x=1 to x=4

2. Find the volume obtained when each of the region is rotated about the y-axis.
a) Under y= x², and the y-axis from x=0 to x=2
b) Under y= x³, and the y-axis from y=1 to y=8
c) Under y= √x, and the y-axis from y=1 to y=2

 LENGTH OF A CURVE

Consider the curve

Example

Find the length of the part of the curves given between the limits:

NEXT TOPIC

Download our APP from Google Playstore using the link CLICK HERE

Join Our Telegram Group for Daily Updates CLICK HERE